Contents:
- Whats is number system?
- What is base?
- What is place value?
What is number system?
A number system is a system of expressing numerical values using distinct symbols or digits. Digits are symbols like 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 used to represent different values of numbers. For example, 1234, 1101, 2FD etc.
Classification of Number System
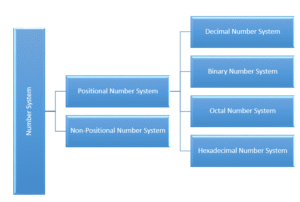
Here, we are more concerned about positional number system. So, we will learn about positional number system and its types only.
A positional number system, also known as place-value system, is a method of representing numbers where each digit in the number has a value depending on its position (called place value) within that number. Each digit in a number has a specific position, starting from rightmost digit as position 0, 1, 2, and so on. To find out place value of a digit in a number, it is necessary to multiply that digit with base (also called the radix, is the total number of unique symbols which can be used to represent the numbers in a given number system) raised to the power of its position.
What is base?
Base (also called the radix) is the total number of unique symbols which can be used to represent the numbers in a given number system. For example, base equals to 4 implies that there are 4 different symbols in that number system. Similarly, base equals to “r” implies that there are “r” different symbols in that number system. Base determines the place value of each digits in the number in a positional number system. When writing numbers in different bases, a subscript is often used to indicate the base, for example, (423)10.
What is place value?
Place value refers to the value of a digit based on its position within a number. For example, in the number (145)10 , at position 0 there is a digit 5, at position 1 the digit 4 is there and the digit 5 is at position 2. As we know that the number is written in decimal number system having base 10. So, the place value of digit 5 at position 0 = (5×100) = 5. The place value of digit 4 at position 1 = (4×101) = 4, and the place value of digit 1 at position 2 = (1×102) = 100. So, to determine the quantity that the number represents, it is necessary to multiply each digit by an integer power of base and then form the sum of all weighted digits. Hence, (145)10=1×102 + 4×101 + 5×100.
🙂 Happy Learning !